നിങ്ങൾ ഒരു ഫുട്ബോൾ അല്ലെങ്കിൽ ക്രിക്കറ്റ് മത്സരം ടിവിയിൽ കാണുകയാണെന്ന് കരുതുക. സമ്പ്രേഷണം ആരംഭിക്കുമ്പോൾ സ്റ്റേഡിയത്തിന്റെ ഒരു ആകാശ വീക്ഷണം ദൃശ്യമാവുന്നു, പിന്നീട് ക്യാമറ സ്റ്റേഡിയത്തിനുള്ളിലേക്ക് കൂടുതൽ വ്യക്തമായ ദൃശ്യങ്ങളിലേക്ക് വരുന്നു. മത്സരം ആരംഭിക്കാൻ പോകുന്നതേയുള്ളൂ. കാണികളുടെ അകലെ നിന്നുള്ള ദൃശ്യം വലിയ വ്യക്തത തരുന്നില്ല. ചില ഭാഗത്ത് ആവേശം തിരതല്ലുന്നു, ചിലർ മെക്സിക്കൻ വേവ് തുടങ്ങി വയ്ക്കുന്നു, അങ്ങിനെ ചില ദൂരക്കാഴ്ച്ചകൾ. ഇനി ദൃശ്യങ്ങൾ വ്യക്തികളിലേക്ക് വരുമ്പോൾ പല കാഴ്ച്ചകൾ കാണാം - ചിലർ സംസാരിക്കുന്നു, അടുത്തുള്ളവരോട് വരാൻ പോകുന്ന മത്സരത്തിന്റെ ആവേശം പങ്ക് വയ്ക്കുന്നു, അങ്ങിനെ അങ്ങിനെ ആകപ്പാടെ ഒരു ഉത്സവാന്തരീക്ഷം ….

ഇനി കാണികളിലേക്ക് ക്യാമറ വരുമ്പോൾ പലരുടെയും ഭാവം മാറുന്നത് കണ്ടിട്ടില്ലേ, അതുപോലെ നമ്മൾ ഒരു വസ്തുവിന്റെ ബാഹ്യവീക്ഷണത്തിൽ നിന്ന് ഉള്ളിലേക്ക് കടക്കാൻ ശ്രമിച്ചാൽ അതിനുള്ളിലുള്ള ആറ്റങ്ങൾ, തന്മാത്രകൾ, ഇലക്ട്രോൺ പോലെയുള്ള കണികകൾ ഒക്കെ എങ്ങിനെയായിരിക്കും പെരുമാറുക? ഭൗതിക വസ്തുക്കളെല്ലാം നിർമ്മിച്ചിരിക്കുന്ന കണികകളെ മനസ്സിലാക്കുന്നതിന് ക്വാണ്ടം സിദ്ധാന്തം അനിവാര്യമാണ്. ഈ സിദ്ധാന്ത പ്രകാരം കണികകളോരോന്നും കാണികളേപ്പോലെ വ്യത്യസ്ത സ്വഭാവങ്ങൾ പ്രകടിപ്പിക്കുന്നു. ഇത് എന്താണെന്ന് മനസ്സിലാക്കണമെങ്കിൽ അവയെ വേർതിരിച്ച് വളരെ താഴ്ന്ന ഊഷ്മാവിൽ ഓരോന്നായി നിരീക്ഷിക്കേണ്ടിയിരിക്കുന്നു. നമുക്ക് ഒരു വസ്തുവിന്റെ ബാഹ്യ വീക്ഷണത്തിൽ എല്ലാ കണികകളും ചേർന്ന് സൃഷ്ടിക്കുന്ന സ്വഭാവങ്ങൾ മാത്രമേ ദർശിക്കാനാവു, ഒരു മൈതാനത്ത് മെക്സിക്കൻ വേവ് ദൃശ്യമാകുന്നത് പോലെ! ഇത്തരം പ്രതിഭാസങ്ങളെ നമുക്ക് അളന്ന് തിട്ടപ്പെടുത്താവുന്ന കൊഹിറന്റ് അവസ്ഥകൾ എന്ന് വിളിക്കാം. എന്നാലിത് നമ്മൾ സൂക്ഷ്മ ലോകത്ത് നിന്ന് നാം ജീവിക്കുന്ന ബാഹ്യലോകത്തേക്ക് വരുമ്പോൾ എത്ര മാത്രം ദർശിക്കാനാവുമെന്നത് ക്വാണ്ടം സിദ്ധാന്തത്തിലെ വലിയ ഒരു ചോദ്യമാണ്. ഇത് ഗണിതശാത്രപരമായോ ഭൗതികശാസ്ത്രപരമായോ യാതോരു പ്രശ്നവുമുണ്ടാക്കുന്നില്ലെങ്കിലും സാമാന്യ ബുദ്ധിക്ക് ചിലപ്പോൾ ഗ്രഹിക്കാൻ ബുദ്ധിമുട്ടാണ്.

എന്നിരിക്കലും, നമ്മൾ ദിവസവും കാണുന്ന ലോകത്തിൽ ഇങ്ങിനെയുള്ള അസന്നിഗ്ദാവസ്ഥകളൊന്നും ഇല്ല എന്നത് ശ്രദ്ധേയമാണ്. നമ്മളൊരിക്കലും ഒരാളെ രണ്ട് സ്ഥലത്തു ഒരേ സമയം കാണാറില്ല. അതോടൊപ്പം ഹൈസൻബെർഗ് മുന്നോട്ട് വച്ച അസന്നിഗ്ദാവസ്ഥാ സിദ്ധാന്തം (Uncertainty Principle) മൂലമുള്ള ഏറ്റക്കുറച്ചിലുകളൊന്നും നമുക്ക് ദർശിക്കാനുമാവുന്നില്ല. അതിനൊരു പ്രധാന കാരണം പുറം ലോകത്തിന്റെ നിരീക്ഷണം ക്വാണ്ടം അവസ്ഥകളുടെ പ്രത്യേകതകൾ പലതും ഇല്ലാതാക്കുന്നു. ബാഹ്യലോകവുമായുള്ള സമ്പർക്കം കൊഹിറന്റ് (Coherent) അവസ്ഥയെ നശിപ്പിക്കുന്നു, ആയതിനെ ഡികൊഹിറൻസ് (Decoherence) എന്നും വിളിക്കാം. കൊഹിറന്റ് അവസ്ഥ നിലനിർത്തുക എന്നത് വളരെ ശ്രമകരമാണെങ്കിലും ഇതിന്റെ ദൈർഘ്യം വർദ്ധിപ്പിക്കാനുള്ള ശ്രമങ്ങൾ ഗവേഷകർ ലോകമെങ്ങും നടത്തുകയും, 2013-ൽ അടക്കം പല നോബൽ സമ്മാനങ്ങളും ഈ മേഘലയിലെ പഠനങ്ങൾക്ക് ലഭിക്കുകയും ചെയ്തു. കലർപ്പില്ലാതെ നിലനിർത്താവുന്ന കുറെ പരസ്പരബന്ധിതമായ ക്വാണ്ടം കണികകളെ സൃഷ്ടിച്ചാൽ അവ ഒരു കമ്പ്യൂട്ടർ നടത്തുന്ന ക്രിയകൾ ചെയ്യാൻ നമ്മളെ സഹായിക്കും എന്നതാണ് ക്വാണ്ടം കമ്പ്യൂട്ടറിന്റെ കാതൽ. ഈ കണികകൾ എന്നത് ചിലപ്പോൾ പ്രത്യേകം തയ്യാറാക്കിയ കുറെ ആറ്റങ്ങളിലെ ഇലക്ട്രോണുകളാവാം, പ്രകാശകണികകളാവാം, നാനോമീറ്റർ വലിപ്പത്തിലുള്ള സർക്യൂട്ടിലെ വൈദ്യുതി പ്രവാഹമാകാം, ചില തന്മാത്രകളാവാം… എതായാലും നിർവഹിക്കുന്ന കർമ്മം ഒന്ന് തന്നെ.

കമ്പ്യൂട്ടർ തലയിലെന്ത്?

വളരെ ലളിതമായ അബാക്കസ് മുതൽ വളരെ ദുരൂഹമായ യന്ത്രങ്ങൾ വരെ മനുഷ്യൻ കണക്കുകൂട്ടലുകൾ നടത്താനായി സൃഷ്ടിച്ചിരുന്നെങ്കിലും അവയുടെ പിന്നിലുള്ള ഗണിതസൂത്രം അഥവാ അൽഗോരിതം മനുഷ്യമസ്തിഷ്കത്തിൽ തന്നെ കുടികൊണ്ടിരുന്നു. മനുഷ്യന്റെ എല്ലാ യുക്തിചിന്തകളും അരിസ്റ്റോട്ടിൽ ക്രോഡീകരിച്ചെങ്കിലും അവയെ ഗണിതരൂപത്തിലവതരിപ്പിക്കാമെന്നത് പലരുടെ ആശയങ്ങളിലൂടെ പൂർണ്ണമായത് ജോർജ്ജ് ബൂൾ എന്ന ഐറിഷ് ഗണിതഞ്ജന്റെ കണ്ടെത്തിയ ബൂളിയൻ ആൾജിബ്രയിലെത്തിയപ്പോഴാണ്. അരിസ്റ്റോട്ടിൽ കണ്ടെത്തിയ ബൈനറി യുക്തി ചിന്തകൾ ഇതോടെ യന്തങ്ങളിൽ സന്നിവേശിപ്പിക്കാനുള്ള ശ്രമങ്ങൾ ഫലത്തിലെത്താൻ തുടങ്ങി. എന്നാൽ ഇരുപതാം നൂറ്റാണ്ടിന്റെ ആദ്യ പകുതി വരെ കമ്പ്യൂട്ടറെന്നാൽ യന്ത്രങ്ങൾ പ്രവർത്തിപ്പിച്ച് മനുഷ്യൻ നടത്തുന്ന കണക്കുകൂട്ടലുകൾ എന്ന സ്ഥിതിയായിരുന്നു. അതിനാൽ അതിനുപയോഗിക്കുന്ന അൽഗോരിതങ്ങൾ യന്ത്രത്തേക്കാൾ അതു പ്രവർത്തിപ്പിക്കുന്ന മനുഷ്യ ക്ലെർക്കിന് മനസ്സിലാവുന്ന വിധമായിരുന്നു. അനലോഗ് കമ്പ്യൂട്ടിങ്ങ് എന്ന് വിളിക്കാവുന്ന ഈ രീതി വളരെ ശ്രമകരവുമായിരുന്നു.

ഇരുപതാം നൂറ്റാണ്ടിന്റെ മദ്ധ്യത്തിലേക്കെത്തിയപ്പോൾ ഇലക്ട്രോണിക് യന്ത്രങ്ങളുടെ ആവിർഭാവം മനുഷ്യൻ ചെയ്യുന്ന പ്രവർത്തികൾ യന്ത്രത്തിന് തന്നെ ചെയ്യാമെന്ന അവസ്ഥയിലെത്തിച്ചു. ബൈനറി ഡിജിറ്റൽ ലോജിക് ഉപയോഗിച്ച് പ്രവർത്തിക്കുന്ന ഈ യന്ത്രങ്ങളുടെ സിദ്ധാന്തം അലൻ ടൂറിങ് തന്റെ സൈദ്ധാന്തിക മഷീൻ വഴി ആവിഷ്കരിക്കുക വഴി ലോകം ഇന്ന് കാണുന്ന ഡിജിറ്റൽ വിപ്ലവം ആരംഭിക്കുകയായി. ബൂളിയൻ ബൈനറി ലോജികും, അത് വഴി മനുഷ്യൻ തന്റെ ഗണിതബുദ്ധിയിൽ എടുക്കാനിടയുള്ള എല്ലാ തീരുമാനങ്ങളും ഇതോടെ യന്ത്രത്തിനു വശമായി. ഗോഡൽ, ചർച്ച്, ടൂറിങ്, വോൺ നോയിമാൻ എന്നിവരുടെ പ്രവർത്തനങ്ങളുടെ സാരമായി നമുക്ക് ലഭിച്ചതെന്തെന്നാൽ മനുഷ്യന്റെ യുക്തിക്ക് സാദ്ധ്യമായ ഏത് ഗണിത പ്രശ്നവും ആവശ്യത്തിന് സമയവും, മെമ്മറിയും നൽകിയാൽ യന്ത്രത്തിനും സാധിക്കുമെന്ന മഹത്തായ കണ്ടെത്തലായിരുന്നു. ഈ യന്ത്രത്തെ നമ്മൾ സെൻട്രൽ പ്രോസ്സസിങ് യൂണിറ്റ് (CPU) എന്ന് വിളിക്കുന്നു. സിപിയു ഒരു ക്രിയ എങ്ങിനെ ചെയ്യണം എന്ന നിർദ്ദേശങ്ങൾ നമ്മൾ നൽകുമ്പോൾ ഇൻപുട്ട് മെമ്മറിയിൽ അഥവാ രജിസ്റ്ററിൽ സൂക്ഷിച്ചിരിക്കുന്ന ബൈനറി സംഖ്യാ രൂപത്തിൽ സൂക്ഷിച്ചിരിക്കുന്ന വിവരം പ്രോസ്സസ്സ് ചെയ്ത്ത് ഔട്ട്പുട്ട് രജിസ്തറിൽ ലഭ്യമാക്കുന്നു. അനലിറ്റിക്കൽ എഞ്ചിൻ ആവിഷ്ക്കരിച്ച ചാൾസ് ബാബേജും, അതിന്റെ പ്രോഗ്രാം എഴുതിയ മാഡം അഡ ലവ്ലേസും വിഭാജനം ചെയ്ത കമ്പ്യൂട്ടിങ് യന്ത്രം ഇതോടെ യാഥാർത്ഥ്യമായി.

ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടർ

ഇങ്ങിനെ രൂപം കൊണ്ട കമ്പ്യൂട്ടറിന്റെ അടിസ്ഥാന ഘടകം വെറും സ്വിച്ചുകളായിരുന്നു. നമ്മൾ റിലേ എന്ന് വിളിക്കുന്ന ഇലക്ട്രോ-മെക്കാനിക്കൽ സ്വിച്ചുകൾ ഉപയോഗിച്ചാണ് ആദ്യകാലത്ത് ഇവ രൂപപ്പെടുത്തിയത്. സ്വിച്ചുകളുടെ വിവിധ ക്രമീകരണങ്ങൾ വഴി യുക്തിസഹമായ എല്ലാ കണക്കുകൂട്ടലുകൾ സാദ്ധ്യമായി. ഈ ക്രമീകരണങ്ങളെ ലോജിക് ഗേറ്റുകൾ എന്ന് വിളിച്ചു. നോട്ട് (NOT), ആൻഡ് (AND), ഓർ (OR), നോർ (NOR), നാൻഡ് (NAND), എക്സ് - ഓർ (XOR), എക്സ് - നോർ (XNOR) എന്നിങ്ങനെ പല പേരുകളാണിവയ്ക്ക്. ഇവയുടെ പലവിധ രൂപങ്ങൾ വിവിധ ഗണിതക്രിയകളും (Aritmetic Operations), യുക്തിക്രിയകളും (Logical Operations) നിർവഹിക്കാൻ ഒരു കമ്പ്യൂട്ടറിനെ പര്യാപ്തമാക്കുന്നു. നാൻഡ് അല്ലെങ്കിൽ ഗേറ്റുകൾ മാത്രം ഉപയോഗിച്ച് ഒരു കമ്പ്യൂട്ടർ പൂർണ്ണമായി നിർമ്മിക്കാവുന്നതേയുള്ളൂ. കാലം മുന്നോട്ട് പോയപ്പോൾ സിലിക്കൺ ട്രാൻസിസ്റ്ററുകൾ സ്വിച്ചുകൾ ആയി പ്രവർത്തിക്കാൻ തുടങ്ങിയെങ്കിലും ലോജിക് മാറിയില്ല. ഇതേ ട്രാൻസിസ്റ്ററുകളോ അവയുടെ രൂപഭേദങ്ങളോ കമ്പ്യൂട്ടറുകളുടെ മെമ്മറിയായും രൂപപ്പ്പെടുത്താമെന്ന് വന്നു. ക്രമേണ ട്രാൻസിസ്റ്ററുകളുടെ എണ്ണം വർദ്ധിച്ച് ഇലക്ട്രോണിക് ചിപ്പുകളിൽ നൂറ് കോടിയിലധികം സ്വിച്ചുകളും മറ്റും നിർമ്മിക്കാമെന്നതോടെ കണക്കുകൂട്ടലുകളുടെ വേഗത ആദ്യകാലത്തേതിൽ നിന്ന് വിശ്വസിക്കാനാവാത്ത തരത്തിൽ വർദ്ധിച്ചു. എങ്കിലും ഇതിന്റെ പരമാവധി വേഗത എത്ര വേഗത്തിൽ ഈ സ്വിച്ചുകളെ ഓൺ/ഓഫ് ആക്കാം എന്നതിനെ ആശ്രയിച്ചിരിക്കുന്നു.

ഇതൊക്കെയാണെങ്കിലും കമ്പ്യൂട്ടർ അപ്പോഴും അതിനു കണക്കുകൂട്ടലുകളുടെ വഴി പറഞ്ഞ് കൊടുക്കുന്ന പ്രോഗ്രാമുകളുടെ അടിമ തന്നെയായിരുന്നു. അൽഗോരിതം പറയുന്ന വഴിക്കേ അത് ചരിക്കൂ. അൽഗോരിതം നന്നല്ലെങ്കിൽ കണക്കുകൂട്ടലുകളും ഒരു വഴിക്കാകും. അൽഗോരിതം അപ്പോഴും ഒരു സിപിയു എങ്ങിനെ ഒരു പ്രശ്നം പരിഹരിക്കണം എന്ന് മാത്രമേ ചിന്തിക്കുന്നുള്ളൂ. ഒരു സമയം ഒരു ഉത്തരം മാത്രമേ അതിന്റെ ഔട്ട് പുട്ടിൽ ലഭിക്കുന്നുള്ളൂ. ഒരേ സമയം സാദ്ധ്യമായ എല്ലാ ഉത്തരങ്ങളും സൂക്ഷിച്ച് വച്ച് നമുക്ക് കരണീയമായ ഉത്തരം തരുന്ന ഒരു കമ്പ്യൂട്ടർ ഉണ്ടെങ്കിൽ നന്നായിരിക്കുമോ? പക്ഷേ അങ്ങിനെ ഒന്നുണ്ടെങ്കിൽ അവയ്ക്ക് അന്യൂനമായ ഓർമ്മശക്തി വേണ്ടി വരില്ലേ?

വിചിത്രമോ ക്വാണ്ടം?

ക്വാണ്ടം ലോകം സാമാന്യ യുക്തിക്ക് വിചിത്രമായി തോന്നാം. പക്ഷേ ശാസ്ത്രത്തിന് ഇന്നതിൽ വിചിത്രമായൊന്നുമില്ല. കാണാവുന്ന പ്രപഞ്ച പ്രതിഭാസങ്ങളൊക്കെ ക്വാണ്ടം സിദ്ധാന്തത്തിനു വഴങ്ങും. അത് പക്ഷെ കൂടുതൽ തെളിച്ചത്തോടെ കത്തുന്നത് ആറ്റങ്ങളുടെയും, തന്മാത്രകളുടെയും ലോകത്തും അതിനേക്കാൾ ചെറിയ വസ്തുക്കളുടെ കാര്യത്തിലുമൊക്കെയാണെന്ന് മാത്രം. അവിടെ നിന്ന് പ്രപഞ്ച പ്രതിഭാസങ്ങളുടെയെല്ലാം യുക്തി വിവരിക്കാനും, താഴെ തട്ടിൽ നിന്നതിന്റെ കാരണം നിർവചിക്കാനും, ക്വാണ്ടം സിദ്ധാന്തത്തിനിന്ന് സാധിക്കുന്നു. മനുഷ്യയുക്തിക്ക് മനസ്സിലാക്കാൻ കഴിയുന്ന കാര്യങ്ങൾക്കും, നിരീക്ഷണ പരീക്ഷണങ്ങൾക്ക് അളന്ന് തിട്ടപ്പെടുത്താനും കഴിയുന്ന കാര്യങ്ങൾക്കേ ശാസ്ത്രത്തിൽ സ്ഥാനമുള്ളൂ എന്ന് കൂടി ഈ വേളയിൽ ചേർത്ത് വായിക്കേണ്ടതുണ്ട്. ഈ സിദ്ധാന്തത്തിന്റെ ഫലങ്ങൾ ഇന്ന് നാം ഉപയോഗിക്കുന്ന മിക്കവാറും ടെക്നോളജിയുടെയും പിന്നിൽ പ്രവർത്തിക്കുമുന്നുമുണ്ട്.

ക്വാണ്ടം ലോകത്തിന്റെ ഒരു പ്രത്യേകതയെന്തെന്നാൽ അതിലുള്ള കണങ്ങളും മറ്റും കൃത്യമായും ഏതവസ്ഥയിലായിരിക്കും എന്ന് പൂർണ്ണമായി പ്രവചിക്കാൻ ഒരു ഉപകരണത്തിനും സാധിക്കില്ല എന്നതാണ്. ഒരു കണം അതിന് സാധ്യമായ എല്ലാ അവസ്ഥകളുടെയും ഒരു സമാഹാരമാണെന്ന് നമുക്ക് കരുതേണ്ടി വരും. എന്നാൽ അതിനെ നമ്മൾ നോക്കി തിട്ടപ്പെടുത്താൻ ശ്രമിച്ചാൽ അത് ഏറ്റവും സാദ്ധ്യതയുള്ള അവസ്ഥയിലേക്ക് രൂപാന്തരപ്പെടുന്നു. അതായത് ആരും എത്തി നോക്കാത്ത ഒരു കലർപ്പുമില്ലാത്ത ഒരു ക്വാണ്ടം ലോകമുണ്ടെങ്കിൽ അതിലെല്ലാ സാദ്ധ്യതകളും കൂടിക്കലർന്നിരിക്കുന്നു എന്ന് കരുതാം. ഈ അവസ്ഥയിൽ കഴിയുന്ന നിരവധി കണങ്ങളുണ്ടെങ്കിൽ അവരെല്ലാം കൂടി ഒരു പ്രത്യേക അവസ്ഥാവിശേഷം കൈവരിക്കുന്നതായും കരുതാം. ഇതിനെ കൊഹിറന്റ് അവസ്ഥയെന്നും, പരസ്പരം വിവരങ്ങൾ പങ്ക് വച്ച് കൊഹിറൻസ് (Coherence) പാലിക്കുന്ന ആ രീതിക്ക് എന്റാംഗിൾമെന്റ് (Entanglement) എന്നും വിളിക്കാം. ബാഹ്യ ലോകവുമായി ബന്ധം വരുന്ന വേളയിൽ ഡീകൊഹിറൻസ് (Decoherence) സംഭവിച്ച് ഓരോ കണവും ഒരു അവസ്ഥകളിലേക്ക് (Basis states) മാത്രം ചുരുങ്ങുന്ന അവസ്ഥാ വിശേഷം വരുന്നു. അപ്പോൾ എന്റാംഗിൾമെന്റ് നശിക്കുന്നതായി മനസ്സിലാക്കാം.

ക്വാണ്ടം കമ്പ്യൂട്ടിങ്ങ്

ക്വാണ്ടം കമ്പ്യൂട്ടർ ആറ്റം, തന്മാത്ര തുടങ്ങിയ ക്വാണ്ടം അവസ്ഥകളെയാണ്, അല്ലെങ്കിൽ അവയുടെ കൂട്ടായ്മയെയാണ് കണക്കുകൂട്ടലുകൾക്കായി ഉപയോഗിക്കുന്നത്. ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടറിന് ലഭ്യമല്ലാത്ത മൂന്ന് അവസ്ഥാവിശേഷങ്ങളാണ് ക്വാണ്ടം ലോകം ഒരു ക്വാണ്ടം കമ്പ്യൂട്ടറിന് നൽകുന്നത്. സൂപ്പർപൊസിഷൻ, എന്റാംഗിൾമെന്റ്, ക്വാണ്ടം ടണലിങ് എന്നിവയാണത്. സൂപ്പർപൊസിഷൻ എന്നാൽ ക്യുബിറ്റുകൾ ‘0’, ‘1’ എന്നീ ബിറ്റുകൾ കൂടാതെ അവ രണ്ടിനുമിടയിലുള്ള അവസ്ഥയിലും ആകാം. എന്റാംഗിൾമെന്റിൽ വിവിധ ക്യുബിറ്റുകൾ അല്ലെങ്കിൽ ക്വാണ്ടം അവസ്ഥകൾ പരസ്പര ബന്ധം സൂക്ഷിക്കുന്നു എന്നതും, ടണലിങ്ങ് ഒരു അവസ്ഥയിൽ നിന്നും മറ്റൊന്നിലേക്ക് ഒരു വേലി ചാടിക്കടക്കാതെ ഒരു ടണൽ വഴി കടക്കാനുള്ള ക്വാണ്ടം അവസ്ഥകളുടെ കഴിവുമാണ്. ക്വാണ്ടം ടണലിങ് പ്രശ്ന പരിഹാരത്തിലേക്ക് അഥവാ ഉത്തരമായി ലഭിക്കേണ്ട അവസ്ഥയിലേക്ക് പെട്ടെന്നെത്താൻ ക്വാണ്ടം കമ്പ്യൂട്ടറിനെ സഹായിക്കുന്നു.

ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടറിൽ ഒരു ബിറ്റ് എന്നാൽ രണ്ട് അവസ്ഥകൾ മാത്രമാണ് - ‘0’ അല്ലെങ്കിൽ ‘1’. ഒരു ട്രാൻസിസ്റ്ററിൽ ഇത് വൈദ്യുതിയുടെ ഉയർന്നതും താണതുമായ രണ്ട് വോൾട്ടേജ് നിലകളാവാം. രണ്ട് ബിറ്റുകൾ ഉണ്ടെങ്കിൽ നമുക്ക് ‘00’, ‘01’ ‘10’, ‘11’ എന്നീ നാല് സാദ്ധ്യതകൾ ഉണ്ടാവുന്നു. എന്നാലിവ നാലു സംഖ്യകൾ എന്നതിനപ്പുറം ഒരു 2-ബിറ്റ് കമ്പ്യൂട്ടറിൽ മറ്റൊന്നിനെയും സൂചിപ്പിക്കുന്നില്ല. അതായത് അതിൽ അടങ്ങിയിരിക്കുന്ന വിവരം (Information) നാലു ബിറ്റ് മാത്രമാണ്. ഒരു ക്യുബിറ്റ് ക്വാണ്ടം കമ്പ്യൂട്ടർ ആണെങ്കിൽ അവയുടെ സാദ്ധ്യമായ അവസ്ഥ

$\alpha \rvert \uparrow \rangle + \beta \rvert \downarrow \rangle$

എന്ന് സൂചിപ്പിക്കാം. ഇതിൽ $\alpha$, $\beta$ എന്നിവ യഥാക്രമം ഈ ക്യുബിറ്റ് ‘0’, ‘1’ എന്നീ അവസ്ഥകളിലാകാനുള്ള സാദ്ധ്യതയെ കുറിക്കുന്നു. ‘0’ എന്ന ബിറ്റ് ഒരു ഇലക്ട്രോണിന്റെ സ്പിൻ $\rvert \uparrow \rangle$ അവസ്ഥയും ‘1’ എന്ന ബിറ്റ് അതേ ഇലക്ട്രോണിന്റെ $\rvert \downarrow \rangle$ അവസ്ഥയും ആയി സൂചിപ്പിച്ചിരിക്കുന്നു. ഈ സാഹചര്യത്തിൽ ക്വാണ്ടം കമ്പ്യൂട്ടർ ഒരു ആറ്റത്തിലെ ഇലക്രോൺ സ്പിൻ അധിഷ്ഠിതമായി പ്രവർത്തിക്കുന്നെന്ന് മാത്രം. എന്നാൽ ഇത് ഒരു പ്രകാശകണികയായ ഫോട്ടോണിന്റെ പോളറൈസേഷൻ അവസ്ഥയോ, ഒരു അതിചാലക റിങ്ങിലെ വൈദ്യുതപ്രവാഹത്തിന്റെ ദിശയോ ഒക്കെയായും ക്വാണ്ടം കമ്പ്യൂട്ടറുകൾ വിഭാജനം ചെയ്യാവുന്നതാണ്. അതുപോലെ ഇവയെ പ്രോഗ്രാം ചെയ്യുക എന്നത് സാധാരണ ചിപ്പുകളിൽ വൈദുത പ്രവാഹം ബൈനറി കോഡ് ഉപയോഗിച്ച് നിയന്ത്രിച്ചാണെങ്കിൽ ക്വാണ്ടം കമ്പ്യൂട്ടറിലത് മറ്റു ഭൗതിക മാർഗ്ഗങ്ങൾ ഉപയോഗിച്ചായിരിക്കുമെന്ന വ്യത്യാസവുമുണ്ട്. ഉദാഹരണത്തിന് റേഡിയോ തരംഗങ്ങൾ, കാന്തിക മണ്ഡലം ഒക്കെ വ്യത്യസ്ത ക്വാണ്ടം കമ്പ്യൂട്ടർ അവസ്ഥകളിൽ ക്യുബിറ്റുകളെ നിയന്ത്രിക്കാൻ ഉപയോഗിക്കുന്നു.

രണ്ട് ക്യുബിറ്റുകൾ ഉള്ള ഒരു ക്വാണ്ടം കമ്പ്യൂട്ടറിൽ മേൽപ്പറഞ്ഞ രീതി പിന്തുടർന്നാൽ ലഭ്യമായ അവസ്ഥകൾ ഒരു 2-ബിറ്റ് ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടറിനേക്കാൾ അധികമാണെന്ന് കാണാം. അതായത് ഓരോ ബിറ്റുകളുടെ അവസ്ഥ മാത്രം അറിഞ്ഞാൽ പോരാ അവയിൽ ആകാനുള്ള സാദ്ധ്യതയെ സൂചിപ്പിക്കുന്ന നാല് സംഖ്യകൾ കൂടി അറിയണം. അവ നമുക്ക് ഇങ്ങിനെ സൂചിപ്പിക്കാം:

$\alpha \rvert \downarrow \downarrow\rangle +\beta \rvert \downarrow \uparrow-\uparrow\downarrow\rangle+\gamma \rvert \downarrow \uparrow+\uparrow\downarrow\rangle+ \delta \rvert \uparrow \uparrow\rangle$.

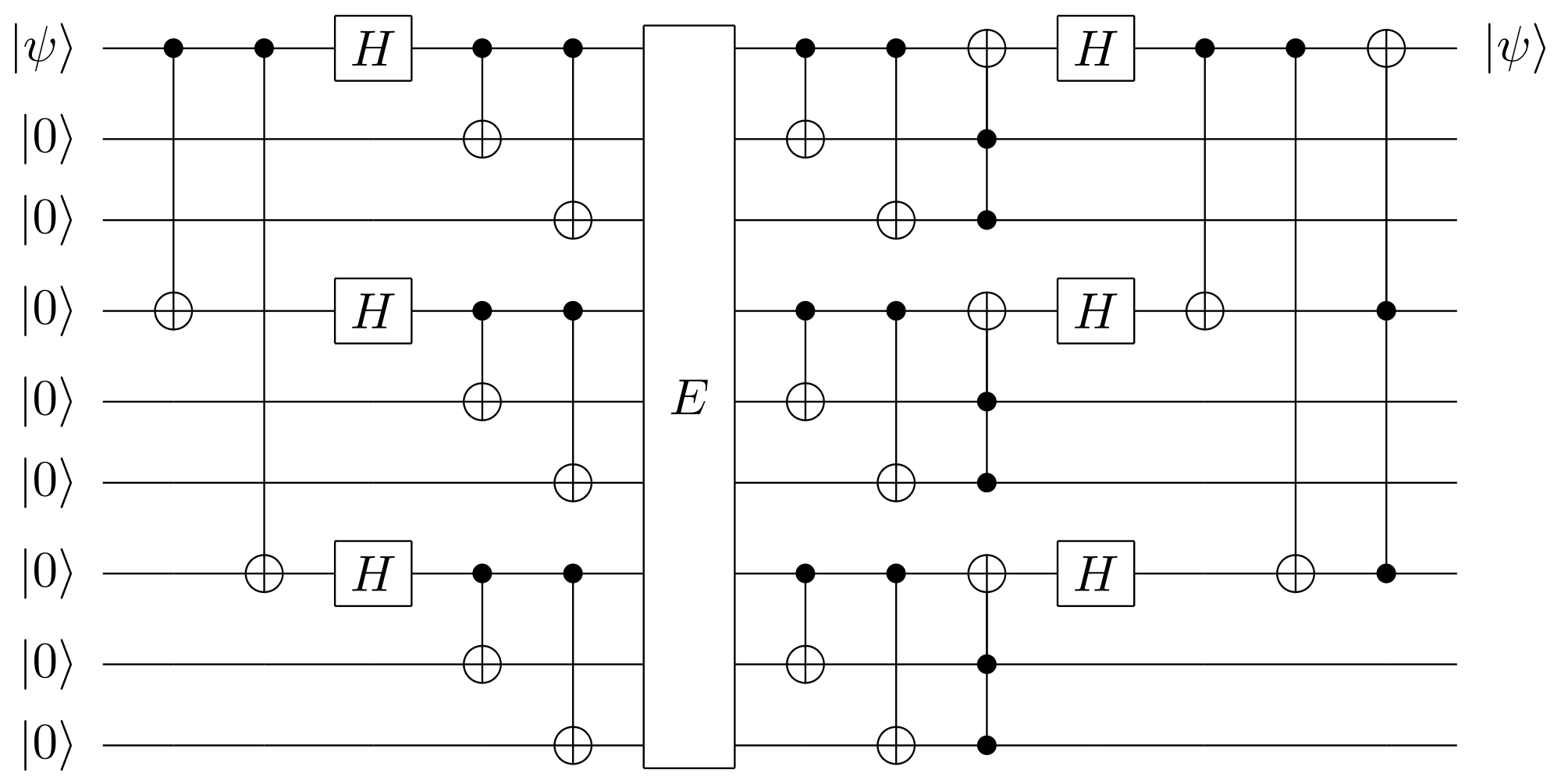
അതായത് രണ്ട് ക്യുബിറ്റുകളിൽ അടങ്ങിയിട്ടുള്ള ക്ലാസ്സിക്കൽ വിവരം $2^2=4$ ആണെന്ന് കാണാം. അപ്പോൾ $N$ ക്യുബിറ്റ് കമ്പ്യൂട്ടറിൽ $2^N$ അടങ്ങിയിരിക്കുന്നു. ഇവ നമുക്ക് ഉപയോഗപ്പെടുത്തണമെങ്കിൽ ക്യുബിറ്റുകൾ എന്റാംഗിൾമെന്റ് അവസ്ഥയിൽ ആയിരിക്കണം എന്ന് മാത്രം.

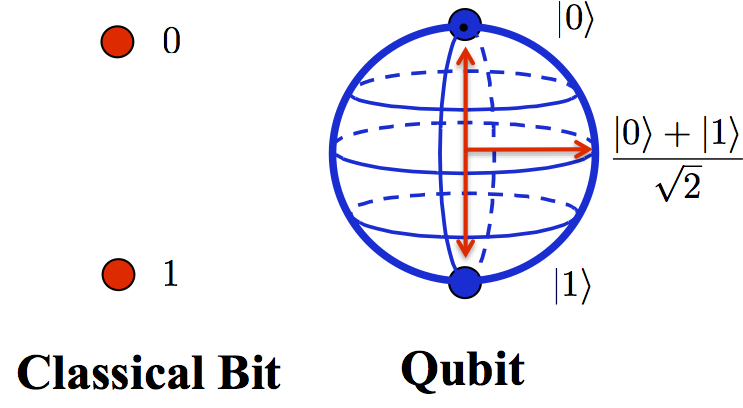
ഒരു ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടറിൽ ബിറ്റുകൾ $0$, $1$ എന്നിവയായിരിക്കെ, അവ രണ്ടും ഒരു മാപ്പിൽ രണ്ട് ബിന്ദുക്കളായി ചിത്രീകരിക്കാം. എന്നാൽ ക്യുബിറ്റുകൾ ഒരു ഗോളത്തിന്റെ, കൃത്യമായി പറഞ്ഞാൽ ബ്ലോക് ഗോളത്തിന്റെ (Bloch sphere), ഉപരിതലത്തിലെ ഒരു ബിന്ദുവായി രേഖപ്പെടുത്താം. അതായത് ചിത്രത്തിൽ കാണുന്നത് പോലെ ഓരോ ക്യുബിറ്റും $\rvert 0\rangle$, $ \rvert 1\rangle$ എന്നീ രണ്ട് അവസ്ഥകളുടെ മിശ്ര അവസ്ഥയായി മനസ്സിലാക്കാം. അത് മാത്രവുമല്ല ഇങ്ങിനെ തയ്യാറാക്കുന്ന നിരവധി ക്യുബിറ്റുകൾ അടങ്ങിയ ഒരു മാദ്ധ്യമം എല്ലാ ക്യുബിറ്റുകളുടെയും വിവിധ അവസ്ഥകളുടെ ഒർ സമ്മിശ്രാവസ്ഥയായി (Superposition) മാറുന്നു. ഒരു ക്വാണ്ടം കമ്പ്യൂട്ടർ ഇക്കാരണത്താൽ വളരെ ശക്തിയുള്ളതായി മാറുന്നു - എല്ലാ അവസ്ഥകളും സൂക്ഷിക്കാം, കൂടാതെ അവയോരോന്നിലും നടത്തുന്ന വ്യതിയാനങ്ങൾ മറ്റുള്ളവയെ ബാധിക്കാതെ ചെയ്യാനും സാധിക്കും. 300 ക്യുബിറ്റുകളുള്ള ഒരു ക്വാണ്ടം കമ്പ്യൂട്ടറിന് ഇക്കാരണത്താൽ ഈ പ്രപഞ്ചത്തിലുള്ള മൊത്തം ആറ്റങ്ങളുടെയും എണ്ണത്തിനു തുല്യമായ അവസ്ഥകൾ സൂക്ഷിക്കാൻ സാധിക്കും. പക്ഷേ, ഇതുപയോഗിച്ച് കണക്കു കൂട്ടലുകൾ നടത്താൻ നാമിനിയും പഠിച്ചു കൊണ്ടിരിക്കുന്നതേയുള്ളൂ!

ക്വാണ്ടം കമ്പ്യൂട്ടർ

``ഒരു ചിപ്പിൽ നിർമ്മിക്കാവുന്ന ട്രാൻസിസ്റ്ററുകളുടെ എണ്ണം ഓരോ പതിനെട്ട് മാസവും ഇരട്ടിയായി വർദ്ധിക്കും”” - ഗോർഡൻ ഏൾ മൂർ

മൂറിന്റെ ഈ നിയമം ഏതാണ്ട് അൻപത് വർഷക്കാലം നിലനിന്നെങ്കിലും ഇന്ന് എല്ലാ ചിപ്പ് നിർമ്മാതാക്കളും ഒരേ പോലെ സമ്മതിക്കുന്ന കാര്യമാണ് ട്രാൻസിസ്റ്ററുകളുടെ വലിപ്പം കുറയ്ക്കുക എന്നത് ഏതാണ്ട് അസാദ്ധ്യമായി മാറിയിരിക്കുന്നു എന്നത്. ട്രാൻസിസ്റ്ററുകളുടെ വലിപ്പം കുറഞ്ഞ് വന്ന് ഏതാനും ആറ്റങ്ങളുടെ വലിപ്പത്തിലായി മാറിയിരിക്കുന്നു. അതിലും ചെറുതാകുന്നത് ഒരു അവയുടെ പ്രവർത്തനം ഇപ്പോഴത്തെ ഇലക്ട്രിക്, ഇലക്ട്രോണിക് നിയമങ്ങൾ പാലിച്ച് പ്രവർത്തിക്കാതെ വരും. ആറ്റോമിക് തലം മുതൽ താഴോട്ടു ക്വാണ്ടം പ്രഭാവം അവയുടെ പ്രവർത്തനത്തെ ബാധിക്കുകയും അവയിലൂടെയുള്ള ഇലക്ട്രോണുകളുടെ ഒഴുക്ക് നിയന്ത്രിച്ച് ചിപ്പുകളുടെ ഇന്നത്തെ പ്രവർത്തന ലക്ഷ്യങ്ങൾ നേടാനാവാതെ പോവും എന്നതാണ് പ്രധാന പ്രശ്നം. ഇതിനൊരു പരിഹാരം എന്ന നിലയിലും, ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടിങിനൊരു മറുവഴി എന്ന വഴിക്കുമൊക്കെ ക്വാണ്ടം കമ്പ്യൂട്ടർ കടന്നു വരുന്നു.

ഇന്ന് ഒരു ക്വാണ്ടം കമ്പ്യൂട്ടറിന് ചെയ്യാൻ കഴിയുന്ന കണക്കുകൂട്ടൽ $3\times 5=15$ പോലെയുള്ള ലളിതമായ കാര്യങ്ങളാണ്. പക്ഷേ ഇത് ചെയ്യാൻ ഏതാനും ആറ്റങ്ങൾ മതിയെന്ന് പറയുമ്പോഴാണ് ഇതിലെ അത്ഭുദം അടങ്ങിയിരിക്കുന്നത്. ഇലക്ട്രോണിക് ചിപ്പുകൾ അവയുടെ നിർമ്മാണ പരിമിതിയുടെ അങ്ങേയറ്റം കണ്ടിരിക്കുകയാണിന്ന്. ട്രാൻസിസ്റ്ററുകളുടെ വലിപ്പം കുറഞ്ഞ് വന്ന് ഏതാനും ആറ്റം വലിപ്പമേ അവയ്ക്കുള്ളൂ എന്ന നിലയിലായിരിക്കുന്നു. അതിൽ ചെറുതായാൽ ക്വാണ്ടം പ്രതിഭാസങ്ങൾ കടന്ന് വരികയും അവയുടെ നാളിതുവരെ അനുഷ്ഠിച്ച് പോരുന്ന ക്ലാസ്സിക്കൽ ധർമ്മങ്ങൾ നിറവേറ്റാനാകാതെയും വരും. അവിടെയാണ് ആറ്റങ്ങളും, തന്മാത്രകളുമൊക്കെ ഉപയോഗിച്ചുള്ള ക്വാണ്ടം കമ്പ്യൂട്ടറുകളുടെ പ്രസക്തി വർദ്ധിക്കുന്നത്. ക്വാണ്ടം പ്രതിഭാസങ്ങൾ ഉപയോഗിച്ചുള്ള ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടർ അവിടെ നമുക്ക് കൈവരിക്കാനാവുന്നു. വേഗത വളരെ വർദ്ധിക്കുന്നു.

ഇവിടെ നിർമ്മിക്കുന്ന ലോജിക് ഗേറ്റുകൾ ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടറിലേത് തന്നെയാണെങ്കിലും, ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടറിലെ തിരിച്ചും മറിച്ചും (Reversible) ഉപയോഗിക്കാവുന്ന എക്സ്-ഓർ (XOR) ഗേറ്റിനു തുല്യമായ നിയന്ത്രിത - നോട്ട് (Controlled - NOT) എന്ന ഒരു ഗേറ്റ് ക്വാണ്ടം കമ്പ്യൂട്ടറിന്റെ പ്രവർത്തനങ്ങൾക്ക് അനിവാര്യമായ ഒന്നാണ്. ഒരു തരത്തിൽ പറഞ്ഞാൽ ലോജിക് ഗേറ്റുകളുടെ ക്വാണ്ടം രൂപമാണ് സിനോട്ട് ഗേറ്റ് എന്ന് പറയാം. ക്വാണ്ടം ക്യുബിറ്റ് അവസ്ഥകളെ എന്റാംഗിൾ (Entangle) ചെയ്യാനും ആ അവസ്ഥയിൽ നിന്നും മാറ്റാനും (Disentangle) സി-നോട്ട് ഗേറ്റുകളെ ഉപയോഗിക്കാം. പ്രധാനമായും ഇതിന് ഇൻപുട്ട് ക്വാണ്ടം അവസ്ഥകളുടെ മിശ്രിത അവസ്ഥ സൃഷ്ടിക്കാൻ സാധിക്കുന്നതിലൂടെയാണിത് സാധിക്കുന്നത്. റിവേഴ്സിബിൾ ഗേറ്റ് ആയതിനാൽ മിശ്രിത അവസ്ഥ വേർതിരിക്കാനും ഇതിനാകുന്നു. ക്വാണ്ടം ടെലിപോർട്ടേഷൻ, ക്വാണ്ടം ക്രിപ്റ്റോഗ്രഫി എന്നിവയിലെല്ലാം ഈ ഗേറ്റുകൾ അനിവാര്യമാണ്.

ക്വാണ്ടം അൽഗോരിതം

ഏതാണ്ട് മുപ്പതോളം വർഷങ്ങൾ ശാസ്ത്രലോകം ഒരു യൂണിവേഴ്സൽ ക്വാണ്ടം കമ്പ്യൂട്ടർ നിർമ്മിക്കാനായി പരിശ്രമം നടത്തി. പക്ഷേ ഇതോടൊപ്പം വികസിച്ച ക്വാണ്ടം അൽഗോരിതങ്ങളൊന്നും ഇത് സ്വായർത്ഥകമാക്കുന്നതായിരുന്നില്ല. എന്നാൽ ചില അൽഗോരിതങ്ങളാവട്ടെ ക്വാണ്ടം കമ്പ്യൂട്ടറിന് ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടറിനേക്കാൽ വളരെ വേഗത്തിൽ ക്രിയകൾ ചെയ്യാൻ സാധിക്കുമെന്ന് കണ്ടെത്തി - പക്ഷേ ചില തെരെഞ്ഞെടുത്തവ മാത്രം. അതിനാൽ തന്നെ ക്വാണ്ടം കമ്പ്യൂട്ടറിന്ന് ക്ലാസിക്കൽ കമ്പ്യൂട്ടറിനൊരു പൂരകമായേ ശാസ്ത്രലോകം കാണുന്നുള്ളൂ.

ക്വാണ്ടം കമ്പ്യൂട്ടർ നിർമ്മിക്കുന്നത് പോലെ തന്നെ പ്രയാസം പിടിച്ച ഒരു പ്രശ്നമാണ് അവയെ എങ്ങിനെ പ്രോഗ്രാം ചെയ്യും എന്നത്. ക്വാണ്ടം മെഷർമെന്റുമായി ബന്ധപ്പെട്ട രണ്ട് നിയമങ്ങളാണിതിന് കാരണം. ഔട്ട് പുട്ട് അളന്ന് കഴിഞ്ഞാൽ സാധ്യമായ എല്ലാ അവസ്ഥകളും ഇല്ലാതായി പകരം ഒരു അവസ്ഥയായി മാറുന്നു. അതിനാൽ ക്വാണ്ടം കമ്പ്യൂട്ടറിന്റെ മുഴുവൻ ശക്തിയും പുറത്തെടുക്കുന്ന അൽഗോരിതങ്ങൾ സൃഷ്ടിക്കാൻ അതിനാൽ തന്നെ പ്രയാസമാണ്. ഇനി അങ്ങിനെയൊന്ന് സൃഷ്ടിക്കാമെന്ന് വച്ചാൽത്തന്നെ ഒരു ക്ലാസ്സിക്കൽ അൽഗോരിതത്തേക്കാൾ ഗണിതശാസ്ത്രപരമായി കൂടുതൽ ദുരൂഹവും സാധാരണ പ്രോഗ്രാമ്മേഴ്സിന് അപ്രാപ്യവുമാണ്.

ആദ്യത്തെ ക്വാണ്ടം അൽഗോരിതം 1994-ൽ പീറ്റർ ഷോർ ആണ് ആവിഷ്ക്കരിച്ചത്. അഭാജ്യ സംഖ്യകളെ പിരിക്കാനുള്ള ഒരു ക്വാണ്ടം അൽഗോരിതമായിരുന്നു ഇത്. 150 അക്കങ്ങളുള്ള ഒരു സംഖ്യയെ പിരിക്കാൻ ഒരു സൂപ്പർകമ്പ്യൂട്ടർ ഏകദേശം ഒരു വർഷം എടുക്കുമെങ്കിൽ ഒരു ക്വാണ്ടം കമ്പ്യൂട്ടറിനിത് ഒരു മാസം കൊണ്ട് സാധിക്കുമെന്ന് ഷോർ അൽഗോരിതം വ്യക്തമാക്കുന്നു. സൈബർ സുരക്ഷയ്ക്ക് ഈ രീതി ഉപയോഗിക്കുന്നതിനാൽ നിലവിലുള്ള സൈബർ സുരക്ഷാ രീതികൾ പൊളിച്ചെഴുതേണ്ട സ്ഥിതി ഇതോടെ വന്നു. ഷോറിനു ശേഷം പുതിയ അൽഗോരിതങ്ങൾ വന്നു. അവ വ്യത്യസ്ഥ പ്രശ്നങ്ങൾ എളുപ്പത്തിലാക്കാനുള്ള വഴികൾ അവതരിപ്പിച്ചു. ഇന്നും ഇത് മികച്ച അൽഗോരിതങ്ങൾ സൃഷ്ടിക്കാനുള്ള പരിശ്രമങ്ങൾ തുടർന്ന് കൊണ്ടേയിരിക്കുന്നു. എന്നാൽ എല്ലാ പ്രശ്നങ്ങളും ഈ രീതിയിൽ മാറ്റാൻ സാധിക്കാത്തതിനാൽ നിലവിലുള്ള ക്വാണ്ടം കമ്പ്യൂട്ടറുകൾ ഒന്നും എല്ലാ പ്രശ്നങ്ങളും പരിഹരിക്കാവുന്ന ടൂറിങ് ഡിജിറ്റൽ കമ്പ്യൂട്ടറുകളല്ല എന്ന് മനസ്സിലാക്കേണ്ടതുണ്ട്. ഈ പ്രത്യേകതകൾ മുൻ നിറുത്തി ഇവയ്ക്ക് സ്വാധീനിക്കാൻ സാധിക്കുന്ന മേഘലകളിൽ ചിലത് താഴെപ്പറയുന്നവയാണ്:

1. മഷീൻ ലേണിങ്
2. ഒപ്റ്റിമൈസേഷൻ
3. സെക്യൂരിറ്റി
4. ഡേറ്റ മൈനിങ്
5. സേർച്ച് അൽഗോരിതം

ക്വാണ്ടം കമ്പ്യൂട്ടർ ചിപ്പ്

1998-ൽ ഒരു സ്റ്റാർട്ടപ്പ് ആയി തുടങ്ങിയ ഡി-വേവ് (D-Wave) എന്ന കനേഡിയൻ കമ്പനി ആണ് ഈ മേഘലയിലെ മുന്നേറ്റക്കാർ. അതിചാലക തത്വം (Supercondcutivity) ഉപയോഗിച്ച് പ്രവർത്തിക്കുന്ന ക്യുബിറ്റുകൾ (qubits) ആണ് ഡി-വേവ് ചിപ്പുകളിൽ ഉള്ളത്. ജോസഫ്സൺ പ്രതിഭാസം (Josephson Effect) മൂലം പ്രവർത്തിക്കുന്ന അതിചാലക സൂക്ഷ്മ റിങ്ങുകളിൽ രണ്ട് ദിശകളിൽ, ഉദാഹരണത്തിന് ഘടികാര ദിശയിലും (clock-wise) അതിന് വിപരീത ദിശയിലും (anti clock-wise), സഞ്ചരിക്കുന്ന വൈദ്യുത കറണ്ട് ‘0’, ‘1’ എന്നീ ക്യുബിറ്റുകളെ സൂചിപ്പിക്കുന്നു. രണ്ടു ദിശയിലും ഒരേ സമയം പ്രവഹിക്കുന്ന കറണ്ട് ഇവയുടെ സമ്മിശ്ര അവസ്ഥയേയും (superposition). 20 മില്ലി കെൽവിൻ ഊഷ്മാവിൽ തണുപ്പിച്ച ഈ ചിപ്പിൽ 512 ക്യുബിറ്റുകൾ ആണുള്ളത്. റേഡിയോ തരംഗങ്ങളൊ, കാന്തിക മണ്ഡലമോ കടക്കാത്ത രീതിയിൽ സൂക്ഷിച്ചിരിക്കുന്ന ഈ ചിപ്പ് അഡയബാറ്റിക് ക്വാണ്ടം കമ്പ്യൂട്ടിങ്ങ് രീതി ഉപയോഗിക്കുന്നു. പരിഹരിക്കാനുള്ള പ്രശ്നം അഥവാ അൽഗോരിതം സ്റ്റാറ്റിസ്റ്റിക്കൽ മെക്കാനിക്സിലെ ഐസിങ് മോഡൽ പ്രശ്നമായി മാറ്റി പരിഹരിക്കുന്ന രീതിയാണിതിലുള്ളത്. പ്രോഗ്രാം ചെയ്ത് കഴിഞ്ഞാൽ ക്യുബിറ്റുകൾ ആ പ്രശ്നം പരിഹരിക്കാനുള്ള രൂപത്തിലേക്ക് മാറുന്നു. ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടറിൽ നിന്ന് വ്യത്യസ്തമായി ഇവിടെ സോഫ്റ്റ്വെയർ ഹാർഡ്വെയറിനെ തന്നെ പ്രശ്നപരിഹാരത്തിനുള്ള രൂപത്തിലേക്ക് (Topology) മാറ്റുന്നു. ഇത് കുറഞ്ഞ വഴിയിലൂടെ പ്രശ്നം പരിഹരിക്കാൻ ക്വാണ്ടം ചിപ്പിനെ സഹായിക്കുന്നു. ഇതിന്റെ വിലയാവട്ടെ വെറും 15 മില്യൺ യുഎസ് ഡോളർ മാത്രം!

അരക്കഴഞ്ച് ഭാവനയും, അരക്കഴഞ്ച് പ്രായോഗികതയും

ഒരു ശാസ്ത്ര നോവലിൽ പ്രതീക്ഷിക്കാവുന്ന ഒരു യന്ത്രമാണെന്ന് തോന്നാമെങ്കിലും ലോകത്തെ പ്രധാന കമ്പനികളും, ഗവേഷണ സ്ഥാപനങ്ങളൂം, പ്രധിരോധ സ്ഥാപനങ്ങളുമൊക്കെ ക്വാണ്ടം കമ്പ്യൂട്ടർ ഗവേഷണത്തിൽ ശ്രദ്ധ പതിപ്പിക്കുമ്പോ ഇതിലെന്തോ കാര്യമുണ്ടെന്ന് തന്നെ കരുതാം. എന്നാൽ ഒരു ക്വാണ്ടം കമ്പ്യൂട്ടർ അടുത്ത കാലത്തെങ്ങാൻ വിപണിയിൽ നമുക്ക് വാങ്ങാൻ ലഭിക്കുമോ എന്ന് ചോദിച്ചാൽ ഇത് മിക്കവാറും ശാസ്ത്രത്തിലെയും, എഞ്ചിനീയറിങ്ങിലെയുമൊക്കെ കടുത്ത പ്രശ്നങ്ങൾ പരിഹരിക്കുന്ന യന്ത്രങ്ങളായും, സാധാരണക്കാർക്ക് ക്ലൗഡ് സേവനം നൽകുന്ന കമ്പ്യൂട്ടറുകളായുമൊക്കെ വരാനെ വഴിയുള്ളൂ. പ്രധാന കാരണം ഇത് സ്ഥിരതയോട് കൂടെ നിലനിർത്തുന്നത് വളരെ പ്രയാസവും ചെലവേറിയതുമാണെന്നതാണ്. ഡികൊഹിറൻസ് സംഭവിച്ച ക്യുബിറ്റുകൾ കൊണ്ട് യാതൊരു പ്രയോജനവും കമ്പ്യൂട്ടറുകൾക്കില്ലാത്തതിനാൽ കൊഹിറൻസ് നിലനിർത്തുന്നത് തന്നെ പ്രധാന ബുദ്ധിമുട്ട്. യാതൊരു വിധ ബാഹ്യ ശക്തികളും ക്യുബിറ്റുകളെ സ്വാധീനിക്കാതെ സൂക്ഷിക്കണം. ഇതിനായി റേഡിയോ തരംഗങ്ങളും കാന്തിക മണ്ഡലവും കടക്കാത്ത, ഉയർന്ന താപം ഡികൊഹിറൻസിടയാക്കാതിരിക്കാൻ വളരെ താഴ്ന്ന ഊഷ്മാവിൽ സൂക്ഷിക്കുന്ന ചിപ്പുകൾ ഉണ്ടാക്കുക ശ്രമകരമാണ്. ക്ലാസ്സിക്കൽ കമ്പ്യൂട്ടറിനൊരു പകരക്കാരനാകാതെ അവയുടെ പ്രവർത്തനം മെച്ചപ്പെടുത്തുന്ന ഒരു പങ്കാളിയായി മാത്രമേ ഇന്നത്തെ നിലയിൽ നമുക്ക് ക്വാണ്ടം കമ്പ്യൂട്ടറിനെ കാണാനാവൂ.

അവലംബം

1. Chip Makers Admit Transistors Are About to Stop Shrinking: https://www.technologyreview.com/s/601962/chip-makers-admit-transistors-are-about-to-stop-shrinking/?utm_campaign=socialflow&utm_source=facebook&utm_medium=post
2. ക്വാണ്ടം കമ്പ്യൂട്ടർ പ്രവർത്തിയ്ക്കുന്നതെങ്ങനെ?: സയൻസ് നോട്ടുപുസ്തകം: https://www.facebook.com/notes/സയൻസ്-നോട്ടുപുസ്തകം/ക്വാണ്ടം-കമ്പ്യൂട്ടർ-പ്രവർത്തിയ്ക്കുന്നതെങ്ങനെ/1818837645006871
3. Google Moves Closer to a Universal Quantum Computer: http://www.scientificamerican.com/article/google-moves-closer-to-a-universal-quantum-computer/
4. Quantum Computing: https://www.bbvaopenmind.com/en/quantum-computing
5. Images from https://en.wikipedia.org/wiki/Quantum_computing under Creative Commons licensing for reuse and modification.

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.